Google Foobar Challenge

I was reading up on dependency injections in Go and saw a “Curious developers are known to seek interesting problems. Solve one from Google?” prompt appear in the Google search bar. In this blog post, I’ll provide solutions to those that I have solved up to the one that I couldn’t.

Reference: Google Foobar

Braille Translation

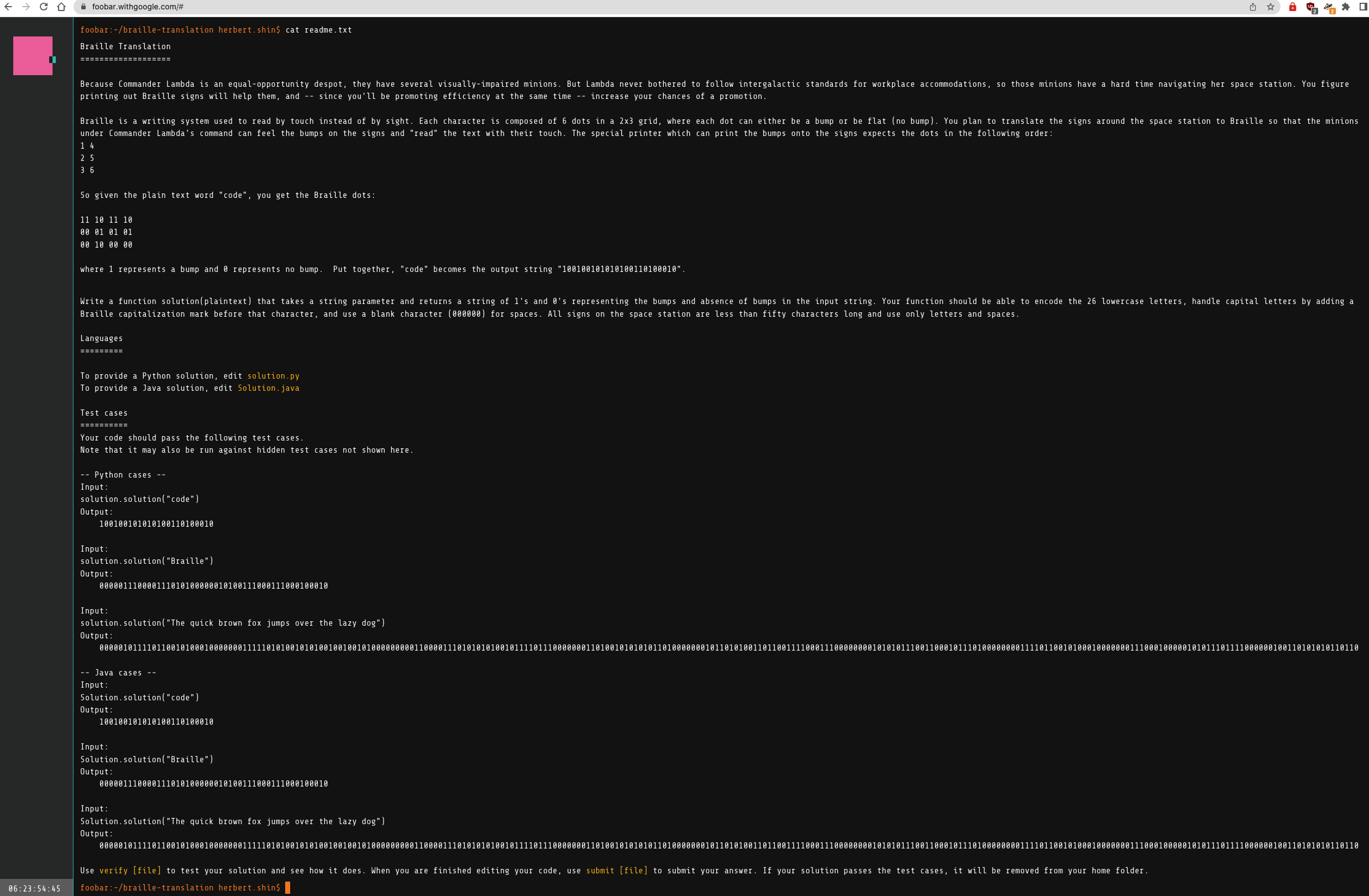
Braille is a reading and writing system for visually impaired people. It’s composed of 6 dots (“Braille cell”) that’s ordered top-down, left-right using bumps and dots as such.

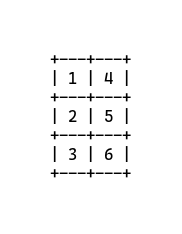
Each of the Braille cells represents a symbol in a natural language. In the foobar challenge, that symbol range was basic Latin alphabets - lowercase and uppercase - and a space. Thankfully, as this constraint allowed me to not consider punctuations, the following table from the Wikipedia Braille article was extremely helpful to solve this problem.

It’s important here to recognize the colors red, green, and purple. The positions 3, 3-6, and 6 act like a control mechanism to provide derivatives to the repeating set: 1, 2, 4, 5. Also interestingly, the ‘w’ is in its own set because the French alphabet did not have that letter when Louis Braille invented the Braille alphabet back in the 1800s! Another interesting observation is that the repeating set doesn’t have these variants.

After trying to read my apartment’s Braille fire escape instructions just using my fingers, I think that’s because it’s difficult to differentiate the above with zero visual guidance. Nonetheless, I decided to hack together a crude replication of the Braille table from Wikipedia and add the problem’s additional capitalization and space constraints.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

BRAILLE_SPACE = '000000'
BRAILLE_CAPITAL = '000001'

BRAILLE_CHARSET = (
    'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j',
    'k', 'l', 'm', 'n', 'o', 'p', 'q', 'r', 's', 't',
    'u', 'v', 'x', 'y', 'z', '',  '',  '',  '',  'w',
)

# After the [a,j] set, the rest are repetitions with only 3rd
# and last bit flipped. So we'll just recycle the base set.
BRAILLE_BITSET = {
    0: ('1', '0', '0', '0', '0', '0'),  # a
    1: ('1', '1', '0', '0', '0', '0'),  # b
    2: ('1', '0', '0', '1', '0', '0'),  # c
    3: ('1', '0', '0', '1', '1', '0'),  # d
    4: ('1', '0', '0', '0', '1', '0'),  # e
    5: ('1', '1', '0', '1', '0', '0'),  # f
    6: ('1', '1', '0', '1', '1', '0'),  # g
    7: ('1', '1', '0', '0', '1', '0'),  # h
    8: ('0', '1', '0', '1', '0', '0'),  # i
    9: ('0', '1', '0', '1', '1', '0'),  # j
}

def BrailleCharacter(char):
    if char == ' ':
        return BRAILLE_SPACE

    c = char.lower()  # lowercase
    i = BRAILLE_CHARSET.index(c) % len(BRAILLE_BITSET)  # index
    b = [*BRAILLE_BITSET.get(i, BRAILLE_SPACE)]  # bitarray

    # Flip bits based on control conditions.
    if c >= 'k':
        b[2] = '1'
    if c >= 'u':
        b[-1] = '1'
    if c == 'w':
        b[2] = '0'

    # Prepend capital bitset if capitalized.
    if char.isupper():
        b.insert(0, BRAILLE_CAPITAL)

    return "".join(b)

def solution(string):
    return "".join([BrailleCharacter(character) for character in string])

Bunny Worker Locations

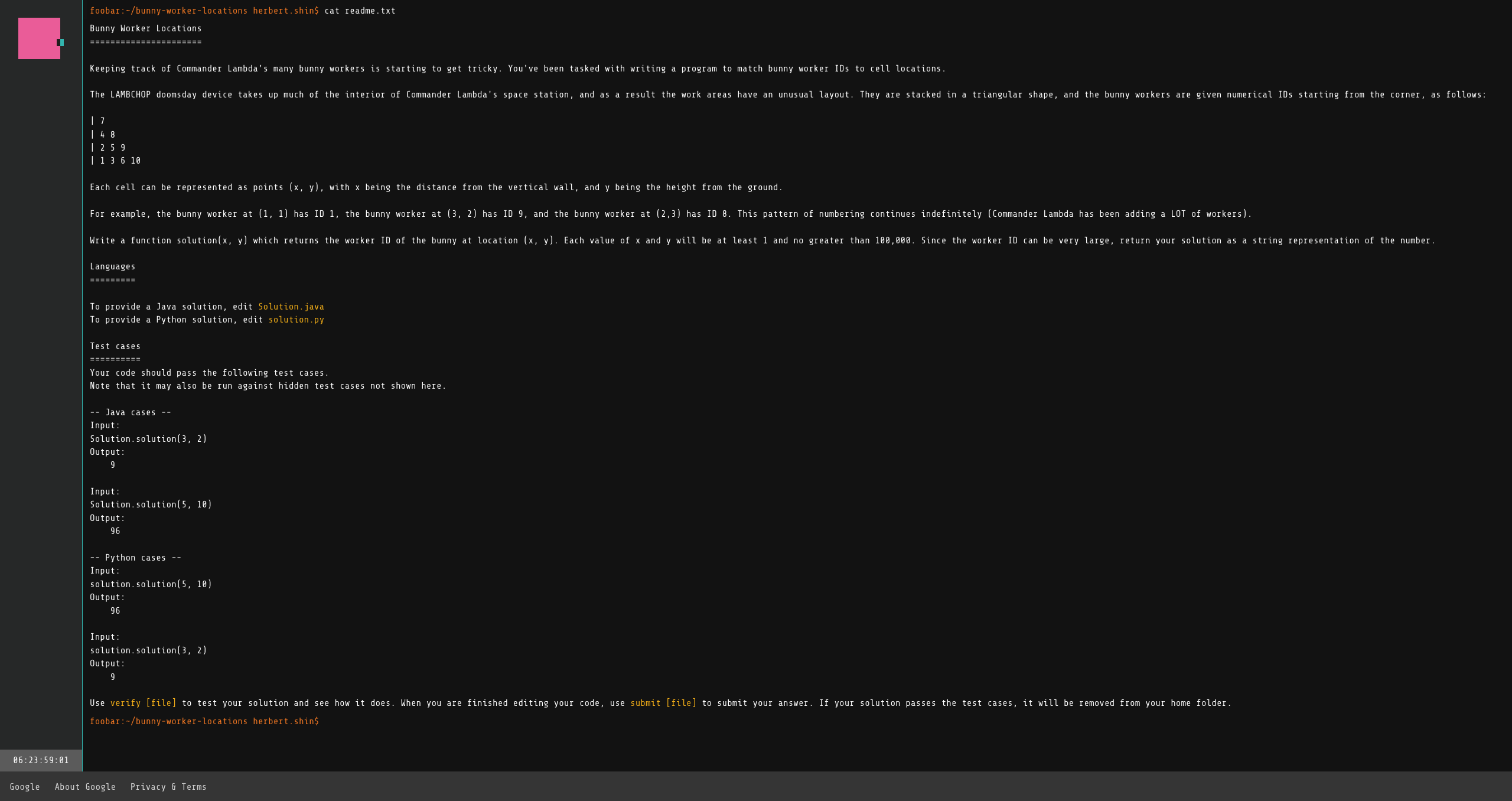
In this problem, we are given a right triangle that’s formed as a successive diagonal series.

The task is to find which number is at (x, y) where x and y are both in (0, 100,000] range as such.

We can use quadratic sequences - but that would require finding the formula for each y set using the difference method. Instead we can observe and tie in a few number patterns to get to a much-faster solution of a constant time.

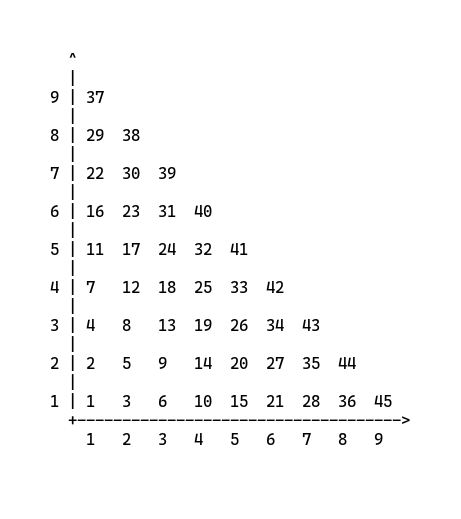
First, as you probably noticed as well, the y=1 number series is basically the addition of the x-axis.

So we can deduce that we can get any xth of y=1 by using this formula.

But this doesn’t accurately reflect if x > 1.

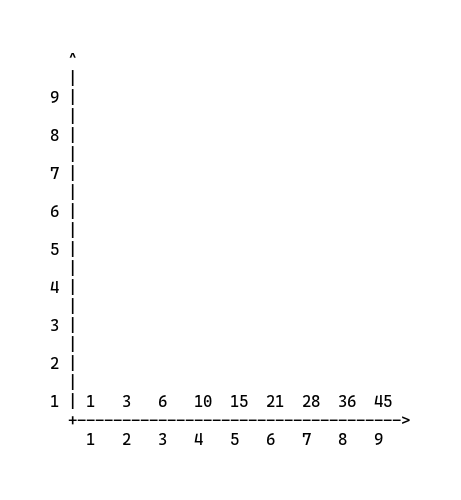
This is another important relationship between the y-axis and x=1.

And as you probably saw it as well, the x=1 is the addition of y-axis minus the last.

So we can deduce that we can get any yth of x=1 by using this formula.

So far we can calculate the “edges” of x and y-axis. Now we just need to add in the organic growth of x * (y-1).

1
2
3
4
5
6
7
8
9

def solution(x, y):
    # I-th x on x-coordinate with y=0 will always be the sum.
    xn = sum(range(1, x+1))

    # Deltas from the y-coordinate growth series.
    yn = sum(range(1, y-1))

    # Organic growth from the y-coordinate.
    return str(xn + yn + (x * (y-1)))

Don’t Get Volunteered!

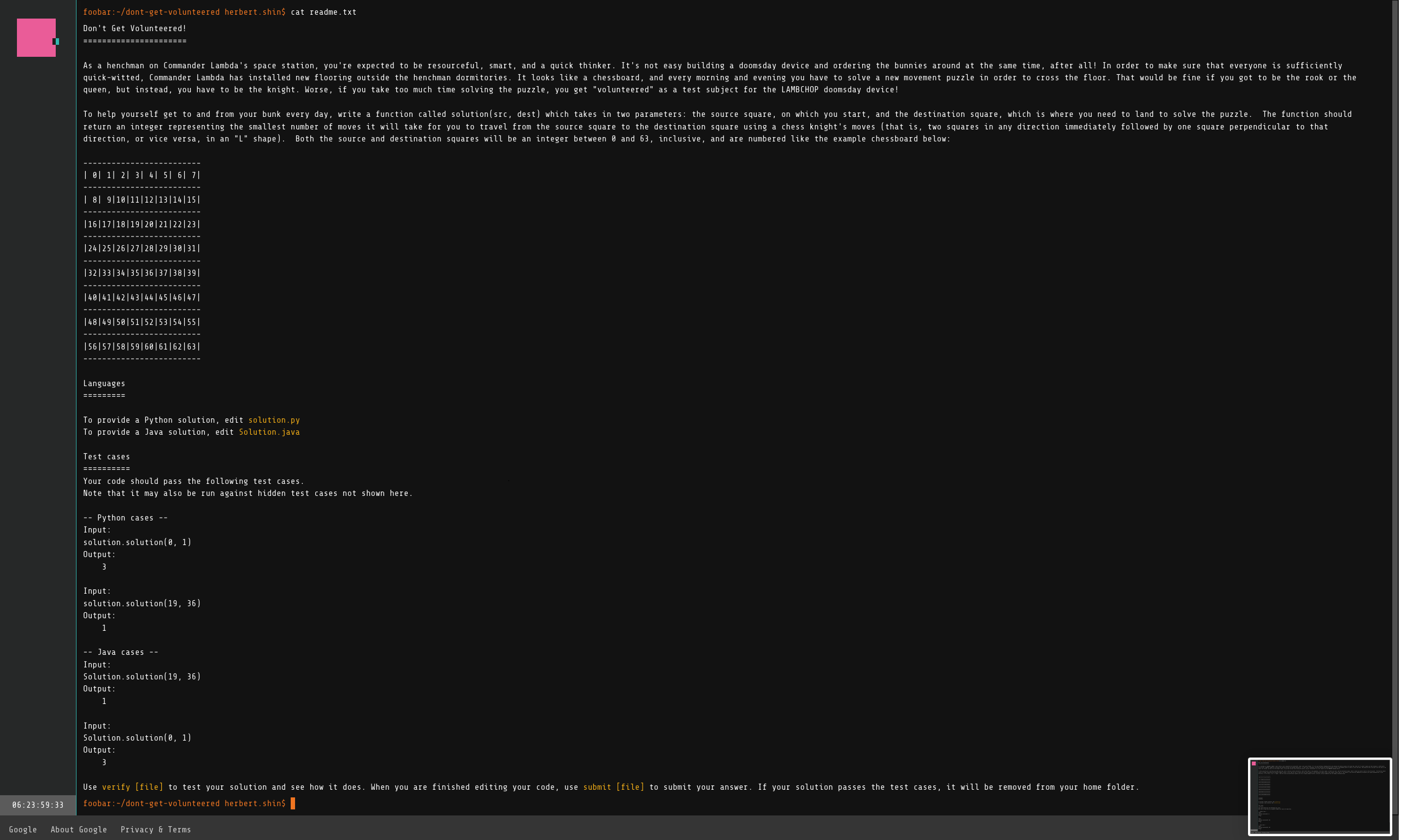
This problem is very similar to a dynamic programming challenge about finding the minimal movement for a knight to get from a position (a, b) to (x, y). However, the difference is that a knight’s starting and end positions are given as an array’s position instead of a 2-dimensional index.

For example, we would need to find the minimum moves from position “5” to “12” instead of (5, 0) to (4, 1).

So aside from the traversal logic, we can get around the above sub-problem by pre-processing the position values to their respective (x, y) coordinates based on the below coordinate mapping.

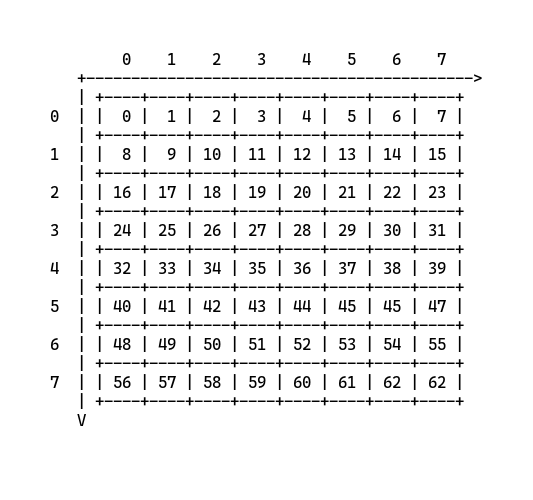
My solution utilizes breadth-first-search (BFS) and coordinate index conversion logic.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

import math

# Relative movements.
KNIGHT_MOVES_DELTA = (
    (-1, -2), (-1, 2), (-2, -1),
    (-2, 1),  (1, -2), (1, 2),
    (2, -1),  (2, 1),
)

def convert_position_to_index(position, rows=8, columns=8):
    return (
        position % columns,                # x
        int(math.floor(position / rows)),  # y
    )

def solution(src, dst):
    # Convert starting and end positions to indexes.
    x1, y1 = convert_position_to_index(src)
    x2, y2 = convert_position_to_index(dst)

    # Initialize visited places of the chess board.
    visited = [[0 for _ in range(8)] for _ in range(8)]

    # Initialize to-be visited places with their cost.
    queue = [((x1, y1), 0)]

    def bfs(x, y, p, q):
        while queue:
            (x, y), cost = queue.pop(0)
            if (x, y) == (x2, y2):
                return cost
            for dx, dy in KNIGHT_MOVES_DELTA:
                _x = x + dx
                _y = y + dy
                if (0 <= _x < 8 and 0 <= _y < 8 and not visitedt[_x][_y]):
                    visited[_x][_y] = 1
                    queue.append(((_x, _y), cost + 1))
    return bfs(x1, y1, x2, y2)

Bomb, Baby!

Unfortunately I was blocked here because I didn’t understand the instructions.

Every Mach bomb retrieves a sync unit from a Facula bomb; for every Mach bomb, a Facula bomb is created;

When I read “X retrieves a sync unit from Y”, I kept thinking about mutexes or semaphores so I wasn’t sure if the “Facula bomb” is an array composed of ‘syncable’ elements and for each pop goes to the “Mach bomb”.

Every Facula bomb spontaneously creates a Mach bomb.

I think here the word “spontaneously” kind of threw me off. The way I interpreted this was if something is spontaneous, that would infer that it’s non-deterministic. So Facula bomb may or may not generate a Mach bomb - which can be expressed using probabilities. But no probability thresholds were given so I was a bit stuck. So my guess is that the challenge wanted to use some kind of generation or genetic algorithms so that I can fully expand on the children of the Mach and Facula bombs.